Решения задач 1-й контрольной работы по теории вероятностей для 803 группы


Один вариант

1. Два равных по силе игрока с начальными капиталами $m$ и $n$ рублей играют в игру, состоящую из отдельных партий. Ничьих не бывает. Проигравший в каждой партии уплачивает выигравшему 1 рубль. Игра продолжается до тех пор, пока один из игроков не отдаст другому последний рубль («разорится»). Найти вероятность разорения каждого из игроков.

Решение. Обозначим через $p_k$ вероятность разорения второго игрока, если у первого начальный капитал равен $k$ рублям. После каждой партии игра начинается заново, меняется лишь начальный капитал. Очевидно, $p_0=0$, $p_{n+m}=1$ и, для $0<k<n+m$,

\begin{displaymath} p_k=\mathsf P(A\,\vert\,B_1)\,\mathsf P(B_1)+\mathsf P(A\,\vert\,B_2)\,\mathsf P(B_2) =\frac{p_{k-1}+p_k}2,\end{displaymath}

где $A=\{$второй игрок разорится$\}$, $B_1=\{$партию выиграл второй игрок$\}$, $B_2=\{$партию выиграл первый игрок$\}$.

То есть $p_0,p_1,\ldots, p_{n+m}$ образуют арифметическую прогрессию с разностью $\delta=1/(n+m)$. Поэтому $p_m=m/(n+m)$.

См., например, Б.В.Гнеденко «Курс теории вероятностей».


2. Имеется последовательность событий $A_1,A_2,\ldots$. С помощью теоретико-множественных операций над событиями записать событие
$B=\{\textit{произойдет бесконечное число событий из последовательности } A_1,A_2,\ldots\}$.


Решение. В данной последовательности произойдет бесконечное число событий в том и только в том случае, если сколь бы большое $N$ мы ни взяли, найдется $k\ge N$ такое, что событие $A_k$ произойдет. Запишем фразу $\{\forall N\,\exists k{\ge}N\,:\, A_k\}$ в терминах операций над событиями:

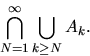
\begin{displaymath} \bigcap_{N=1}^{\infty}\bigcup_{k\ge N} A_k.\end{displaymath}

3. Найти вероятность того, что при случайном размещении $n$ различных шаров по $n$ ящикам ровно один ящик останется пустым.

Решение. Общее число исходов равно $n^n$. Число благоприятных исходов есть число способов разложить $n-2$ шара по одному, оставив один ящик пустым и положив два шара в один ящик. Выберем два шара $C_n^2$ способами, ящик для них $n$ способами, пустой ящик $n-1$ способом, остальные $n-2$ шара разложим $(n-2)!$ способами.

Ответ: $\dfrac{C_n^2\cdot n \cdot (n-1) \cdot (n-2)!}{n^n}$.

4. Известно, что при бросании семи игральных костей выпала по крайней мере одна шестерка. Какова при этом вероятность того, что выпали ровно две единицы?

Решение.

\begin{displaymath} \mathsf P(A\,\vert\,B)=\dfrac{\mathsf P(A\cap B)}{\mathsf P(B)}\,, \quad \mathsf P(B)=1-{\left(\frac{5}{6}\right)}^7.\end{displaymath}

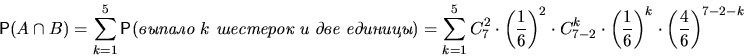
\begin{displaymath} \mathsf P(A\cap B)=\sum_{k=1}^5 \mathsf P(\textit{выпало } k... ...(\frac{1}{6}\right)}^k \cdot {\left(\frac{4}{6}\right)}^{7-2-k}\end{displaymath}

5. Есть 2 урны, в каждой по 10 шариков, причем в какой-то из урн есть красный шар, а остальные 19 шаров белые. Вероятность того, что красный шар находится во второй урне, равна 1/3. Вы можете вынимать шар 15 раз (с возвращением). Сколько раз нужно вынимать шары из первой, и сколько из второй урны, чтобы вероятность извлечь красный шар была наибольшей? Примечание: $\log_{0.9}2=-6.579$.


Решение. Условимся вынимать шар из первой урны $k$ раз, из второй — $15{-}k$ раз. Требуется минимизировать (по $k$) вероятность ни разу не вынуть красный шар. Обозначим это событие через $A$. Пусть $B_i=\{$шар в $i$-й урне$\}$.

\begin{displaymath} \mathsf P(A)= \mathsf P(A\,\vert\,B_1)\,\mathsf P(B_1)+\math... ...mathsf P(B_2)= \frac23 \cdot 0{,}9^k+\frac13\cdot 0{,}9^{15-k}.\end{displaymath}

Минимум функции $\frac23 \cdot 0{,}9^x+\frac13\cdot 0{,}9^{15-x}$ достигается при $x=\frac{15-\log_{0,9}2}{2}\approx 10{,}79$.
Осталось сравнить $\mathsf P(A)$ при $k=10$, $k=11$ и выбрать $k$, при котором вероятность «не вынуть красный шар» меньше.
Ответ: $k=11$.

Еще один вариант

1. Две точки брошены наудачу и независимо друг от друга на отрезок $[0,1]$, $\xi_1$ и $\xi_2$ — координаты этих точек. Описать множество всех значений $r$, при которых независимы события $A=\{\vert\xi_1-\xi_2\vert\ge r\}$ и $B=\{\xi_1+\xi_2\le 3r\}$.

Решение. Заметим сначала, что при $r\le 0$ события $A$ и $B$ независимы, поскольку $A=\Omega$, а при $r\ge 2/3$ события $A$ и $B$ независимы, поскольку $B=\Omega$. При всех $0<r<1$

\begin{displaymath} \mathsf P(A)=(1-r)^2.\end{displaymath}

При $0<r\le\frac13$ (нарисовать квадрат и убедиться)

\begin{displaymath} \mathsf P(B)=\frac{(3r)^2}2, \quad \mathsf P(A\cap B)=2r^2,\end{displaymath}

и события $A$ и $B$ независимы лишь при $r=1/3$.

При $\frac13<r<\frac12$

\begin{displaymath} \mathsf P(\overline B)=\frac{(2-3r)^2}2, \quad \mathsf P(A\cap \overline B)=2(1-2r)^2,\end{displaymath}

и $(1-r)^2\cdot \frac{(2-3r)^2}2=2(1-2r)^2$ лишь при $r=0$ либо $1/3$, так что ни при каком $\frac13<r<\frac12$ события $A$ и $B$ не являются независимыми.

Заметим, что при $\frac12\le r<\frac23$ событие $A$ влечет $B$: $A\subseteq B$. Стало быть, при таких $r$ события $A$ и $B$ не являются независимыми, поскольку вероятность $A$ отлична от нуля, а вероятность $B$ — от единицы.

Ответ: $r\in \bigl(-\infty,0\bigr]\cup \bigl\{\frac13\bigr\}\cup\bigl[\frac23,\infty\bigr)$.

2. Есть 2 урны, в каждой по 10 шаров, причем в какой-то из урн есть красный шар, остальные 19 шаров белые. Вероятность того, что красный шар находится в первой урне, равна 3/4. Вы можете вынимать шар 12 раз (с возвращением). Сколько раз нужно вынимать шары из первой, и сколько из второй урны, чтобы вероятность извлечь красный шар была наибольшей? Примечание: $\log_{0.9}3=-10.427$.

Решение. Условимся вынимать шар из первой урны $k$ раз, из второй — $12{-}k$ раз. Требуется минимизировать (по $k$) вероятность ни разу не вынуть красный шар. Обозначим это событие через $A$. Пусть $B_i=\{$шар в $i$-й урне$\}$.

\begin{displaymath} \mathsf P(A)= \mathsf P(A\,\vert\,B_1)\,\mathsf P(B_1)+\math... ...mathsf P(B_2)= \frac34 \cdot 0{,}9^k+\frac14\cdot 0{,}9^{12-k}.\end{displaymath}

Минимум функции $\frac34 \cdot 0{,}9^x+\frac14\cdot 0{,}9^{12-x}$ достигается при $x=\frac{12-\log_{0,9}3}{2}\approx 11{,}21$.
Осталось сравнить $\mathsf P(A)$ при $k=11$, $k=12$ и выбрать $k$, при котором вероятность «не вынуть красный шар» меньше.
Ответ: $k=11$.

3. Два равных по силе игрока с начальными капиталами $m$ и $n$ рублей играют в игру, состоящую из отдельных партий. Ничьих не бывает. Проигравший в каждой партии уплачивает выигравшему 1 рубль. Игра продолжается до тех пор, пока один из игроков не отдаст другому последний рубль («разорится»). Найти вероятность разорения каждого из игроков.

Решение. См. 1-й вариант.

4. Квадрат горизонтальными линиями разделен на $n$ одинаковых полос. В каждую из них бросается точка, положение которой равновозможно в любом месте полосы. Затем аналогично предыдущему проводят $n-1$ вертикальную линию. Определить вероятность того, что в каждой вертикальной полосе будет только по одной точке.

Решение. Поскольку вероятность каждой точке попасть в любую из $n$ вертикальных полос одинакова и равна $1/n$, то интересующая нас вероятность равна ${n!}/{n^n}$.

5. В урну, содержащую $n$ шаров, опущен белый шар. Какова вероятность извлечь из этой урны белый шар, если все предположения о первоначальном числе белых шаров равновозможны?

Ответ. $\displaystyle\frac{n+2}{2(n+1)}$.


Natalia Chernova
16.10.2000