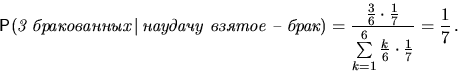Решения задач 1-й контрольной работы по теории вероятностей для 823 группы
Один вариант
1. Из последовательности чисел 1, 2, ..., 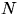 отобраны
отобраны 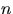 чисел и расположены в порядке возрастания:
чисел и расположены в порядке возрастания:
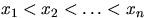 . Какова вероятность того, что
. Какова вероятность того, что 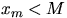 ?
Найти предел этой вероятности, когда
?
Найти предел этой вероятности, когда 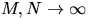 так,
что
так,
что 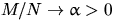 .
.
Решение.
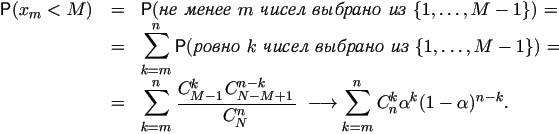
2. На окружности наудачу выбраны две точки 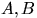 . Найти
вероятность того, что хорда
. Найти
вероятность того, что хорда 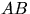 удалена от центра на расстояние
большее половины радиуса.
удалена от центра на расстояние
большее половины радиуса.
Решение.
Зафиксируем точку 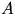 . Хорда
. Хорда 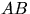 удалена от центра на расстояние
большее половины радиуса в том и только в том случае, когда
она опирается на центральный угол больший
удалена от центра на расстояние
большее половины радиуса в том и только в том случае, когда
она опирается на центральный угол больший 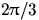 :
:
![$B\in[0,2\pi/3]\cup[4\pi/3,2\pi)$](img12.gif) .
.
Ответ. 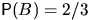 .
.
3. В урне 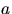 белых и
белых и 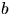 черных шаров. Наудачу извлекается
шар. Он возвращается обратно и, кроме того, добавляется
черных шаров. Наудачу извлекается
шар. Он возвращается обратно и, кроме того, добавляется 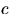 шаров одного с ним цвета. Производится новое извлечение, и
процедура изменения состава урны повторяется. Найти вероятность
извлечения белого шара на
шаров одного с ним цвета. Производится новое извлечение, и
процедура изменения состава урны повторяется. Найти вероятность
извлечения белого шара на 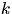 -м шаге.
-м шаге.
Решение.
Вероятность вынуть белый шар на первом шаге равна
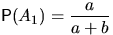 .
.
На втором шаге
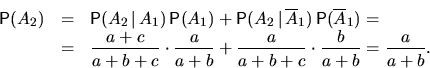
Выскажем предположение: для любого первоначального
состава урны вероятность вынуть белый шар на любом (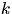 -м)
шаге одинакова и равна доле белых шаров в исходной урне.
-м)
шаге одинакова и равна доле белых шаров в исходной урне.
Докажем его по индукции.
При 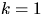 и даже при
и даже при 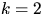 доказано (при произвольных
доказано (при произвольных 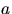 и
и 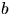 ).
).
Пусть предположение верно при 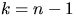 . Заметим, что
. Заметим, что
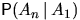 есть вероятность вынуть белый шар
на
есть вероятность вынуть белый шар
на 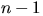 -м шаге из урны, содержащей первоначально
-м шаге из урны, содержащей первоначально 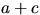 белых
и
белых
и 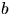 черных шаров. Эта вероятность равна
черных шаров. Эта вероятность равна 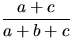 по предположению индукции. Точно так же и
по предположению индукции. Точно так же и
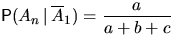 .
Тогда при
.
Тогда при 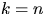
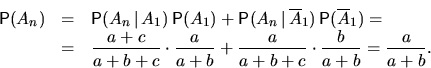
При 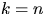 доказано (при произвольных
доказано (при произвольных 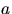 и
и 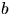 ).
).
4.
Каждое из четырех событий может произойти соответственно
с вероятностями 0.012, 0.010, 0.006 и 0.002. Определить вероятность того,
что в результате опыта произойдет хотя бы одно из этих событий,
если эти события а) несовместны; б) независимы.
Решение.
а) 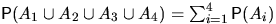 .
.
б)
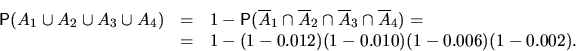
5.
Игральная кость  имеет четыре красных и две белых грани,
а кость
имеет четыре красных и две белых грани,
а кость 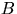 — две красных и четыре белых.
Один раз бросается монета.
Если выпал герб, то все время бросается только кость
— две красных и четыре белых.
Один раз бросается монета.
Если выпал герб, то все время бросается только кость 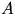 , если решетка — только кость
, если решетка — только кость 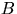 .
.
а) Вычислить вероятность получить красную грань
при одном бросании кости.
б) Известно, что первые два бросания кости дали красные грани.
Найти вероятность того, что третье бросание также даст красную грань.
Решение.
а) 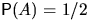 .
.
б) 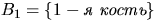 ,
, 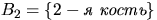 .
.
Еще один вариант
1. Электрическая цепь состоит из элементов 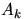 , соединенных
по следующей схеме:
, соединенных
по следующей схеме:
Вероятность выхода из строя элемента 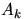 равна
равна 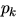 .
Предполагается, что элементы выходят из строя независимо друг от друга.
Найти вероятность того, что цепь будет пропускать ток.
.
Предполагается, что элементы выходят из строя независимо друг от друга.
Найти вероятность того, что цепь будет пропускать ток.
Решение. Цепь работает, если работает 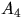 и хоть одна из
линий
и хоть одна из
линий 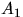 ,
, 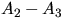 . Пусть
. Пусть 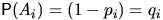 ,
, 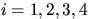 .
.
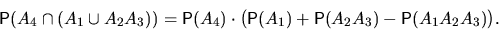
Ответ. 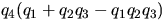 .
.
2. В сфере радиуса 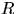 случайно и независимо
друг от друга разбросано
случайно и независимо
друг от друга разбросано 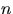 точек.
точек.
Чему равна вероятность того, что расстояние
от центра до ближайшей точки будет не менее 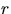 ?
Найти предел этой вероятности,
при
?
Найти предел этой вероятности,
при 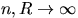 так, что
так, что 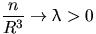 .
.
Решение.
Все точки расположатся вне шара радиуса 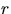 с вероятностью
с вероятностью
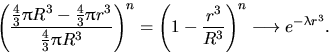
3. Собрались вместе 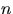 незнакомых человек.
Считая, что день рождения приходится на любой из 365 дней года с равной
вероятностью, найти вероятность того, что хотя бы у двух из них
совпадают дни рождения.
незнакомых человек.
Считая, что день рождения приходится на любой из 365 дней года с равной
вероятностью, найти вероятность того, что хотя бы у двух из них
совпадают дни рождения.
Решение.
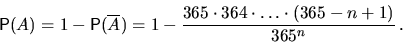
4.
В первой урне 5 белых и 3 черных шара, во второй —
1 белый и 3 черных. Наудачу выбирается урна, и из нее дважды (с возвращением)
выбирается шар.
а) Найти вероятность того, что во второй раз будет вынут белый шар.
б) Найти вероятность того, что во второй раз будет вынут белый шар, если в первый
раз был вынут белый шар.
Решение. См. В. Феллер, т. 1, гл. 5, § 2.
Положим 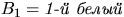 ,
, 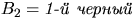 ,
,
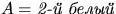 .
.
б)
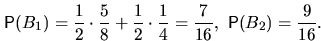
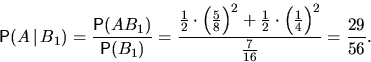
Заметьте, что вероятность 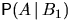 не равна
не равна 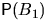 .
.
а)
С очевидностью, 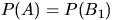 . Действительно, повторяя предыдущие
рассуждения, получим
. Действительно, повторяя предыдущие
рассуждения, получим 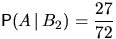 ,
,
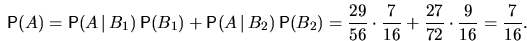
5.
Из партии в шесть изделий наудачу взято одно изделие, оказавшееся
бракованным. Количество бракованных изделий в партии равновозможно любое.
Какова вероятность, что бракованных изделий ровно три?
Решение. Формула Байеса:
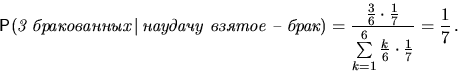
Natalia Chernova
17.10.2000
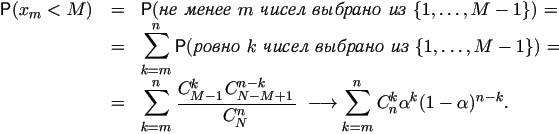
![]() . Хорда
. Хорда ![]() удалена от центра на расстояние
большее половины радиуса в том и только в том случае, когда
она опирается на центральный угол больший
удалена от центра на расстояние
большее половины радиуса в том и только в том случае, когда
она опирается на центральный угол больший ![]() :
:
![]() .
. ![]() .
.
![]() .
. 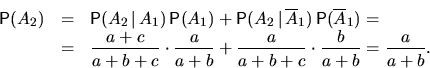
![]() -м)
шаге одинакова и равна доле белых шаров в исходной урне.
-м)
шаге одинакова и равна доле белых шаров в исходной урне.
![]() и даже при
и даже при ![]() доказано (при произвольных
доказано (при произвольных ![]() и
и ![]() ).
).
![]() . Заметим, что
. Заметим, что
![]() есть вероятность вынуть белый шар
на
есть вероятность вынуть белый шар
на ![]() -м шаге из урны, содержащей первоначально
-м шаге из урны, содержащей первоначально ![]() белых
и
белых
и ![]() черных шаров. Эта вероятность равна
черных шаров. Эта вероятность равна ![]() по предположению индукции. Точно так же и
по предположению индукции. Точно так же и
![]() .
Тогда при
.
Тогда при ![]()
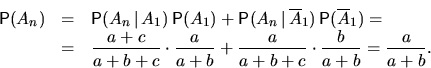
![]() доказано (при произвольных
доказано (при произвольных ![]() и
и ![]() ).
).
![]() .
.
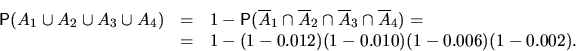
![]() .
.
![]() ,
, ![]() .
.
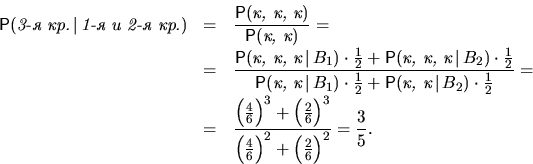
![\begin{picture}
(65,18)(0,-8)
\unitlength=1mm
\put(0,0){\vector(1,0){7}}
\put(7,...
...ox [8\unitlength]{\shortstack{$A_4$}}
}
\put(44,0){\vector(1,0){7}}\end{picture}](img38.gif)
![]() равна
равна ![]() .
Предполагается, что элементы выходят из строя независимо друг от друга.
Найти вероятность того, что цепь будет пропускать ток.
.
Предполагается, что элементы выходят из строя независимо друг от друга.
Найти вероятность того, что цепь будет пропускать ток.
![]() и хоть одна из
линий
и хоть одна из
линий ![]() ,
, ![]() . Пусть
. Пусть ![]() ,
, ![]() .
.
![]()
![]() .
.
![]() ?
Найти предел этой вероятности,
при
?
Найти предел этой вероятности,
при ![]() так, что
так, что ![]() .
.![]() с вероятностью
с вероятностью
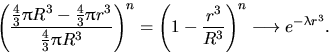
![]()
![]() ,
, ![]() ,
,
![]() .
.
![]()
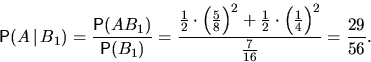
![]() не равна
не равна ![]() .
.
![]() . Действительно, повторяя предыдущие
рассуждения, получим
. Действительно, повторяя предыдущие
рассуждения, получим ![]() ,
,
![]()