
|
Первая контрольная работа по теории вероятностей
2002/2003 учебный год, 20 марта 2003 г.
1 курс ЭФ
|
|
- 1.
- На полке семь учебников по теории вероятностей, семь —
по математическому анализу и одиннадцать — по микроэкономике. Наудачу выбирают
шесть книг. Найти вероятность того, что среди них будет не менее четырех книг
по теории вероятностей.
- 2.
- На отрезок [0,2] наудачу и независимо друг от друга
брошены две точки с координатами
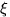 и
и 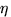 .
Проверить, являются ли события
.
Проверить, являются ли события
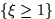 и
и 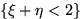 независимыми.
независимыми.
- 3.
- Четырнадцать раз подбрасывается пара игральных костей.
Какова вероятность того, что сумма очков, равная 3, выпадет не менее
пяти, но не более десяти раз?
- 4.
- В первой урне 7 белых и 2 черных шара, во второй —
4 белых и 5 черных, в третьей — 3 белых и 6 черных, и
в четвертой — 2 белых и 7 черных.
Из каждой урны наудачу выбирается шар. Известно, что три шара
оказались белыми и один шар — черным.
Найти (условную) вероятность того, что из второй урны был выбран белый шар.
- 5.
- Из полной колоды карт (52 карты) вынимают одновременно пять
карт. Рассматриваются события:
A={среди вынутых карт есть хотя бы одна пиковая};
B={среди вынутых карт есть хотя бы две бубновых}.
Найти вероятность объединения событий A и B .
- 6.
- Пусть события
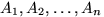 независимы в совокупности.
Доказать, что тогда события
независимы в совокупности.
Доказать, что тогда события 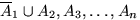 также
независимы в совокупности.
также
независимы в совокупности.
- 1.
- Из урны, содержащей по десять красных, синих и белых шаров,
наудачу и без возвращения выбираются 8 шаров. Найти вероятность того, что
среди них попадутся хотя бы три синих шара.
- 2.
- На отрезок [-1,1] наудачу и независимо друг от друга
брошены две точки с координатами
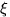 и
и 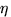 . Проверить, являются ли события
. Проверить, являются ли события
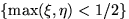 и
и 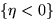 независимыми.
независимыми.
- 3.
- Семь раз подбрасываются три игральные кости.
Какова вероятность того, что сумма очков, равная 17, выпадет не менее
пяти раз?
- 4.
- Игральная кость A имеет четыре красных и две белых грани,
кости B и C — по три красных и три белых,
а кость D — две красных и четыре белых.
Кости брошены один раз, при этом одна кость выпала красной гранью, а
остальные белыми.
Найти (условную) вероятность того, что кость D выпала белой гранью.
- 5.
- Два стрелка, независимо один от другого, делают по три выстрела
каждый по своей мишени. Вероятность попадания в мишень при одном выстреле
для первого стрелка 1/4, для второго — 1/3.
Найти вероятность того, что в мишени первого стрелка будет больше пробоин.
- 6.
- На отрезок [0,1] наудачу и независимо друг от друга
бросаются 5 точек. Обозначим через X(1) координату самой левой точки
(минимальная из координат точек),
и через X(5) — координату самой правой (максимальная из координат).
Доказать, что события
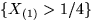 и
и 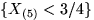 зависимы.
зависимы.
- 1.
- В коробке — по 7 желтых, синих и красных шаров.
Наудачу и без возвращения выбирают 9 шаров. Найти вероятность того, что попадется не более трех синих шаров.
- 2.
- На отрезок [-1,2] наудачу и независимо друг от друга
брошены две точки с координатами
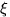 и
и 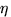 . Проверить, являются
ли события
. Проверить, являются
ли события 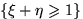 и
и 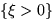 независимыми.
независимыми.
- 3.
- Девять раз подбрасывается пара игральных костей.
Какова вероятность того, что сумма очков, равная 11, выпадет не менее
двух, но не более пяти раз?
- 4.
- Стрелки A , B , C и D попадают по мишени с вероятностями
0,2, 0,6, 0,1 и 0,9 соответственно, независимо друг от друга.
Стрелки дали залп по мишени, и в мишень попали ровно три пули.
Найти (условную) вероятность того, что C попал.
- 5.
- В урне 10 белых и 8 черных шаров. Из урны без возвращения
вынимают 7 шаров.
Найти вероятность того, что среди вынутых шаров будет больше белых,
чем черных.
- 6.
- Колода карт (52 карты) раздается поровну четырем игрокам — по 13 карт
каждому. Найти вероятность того, что хотя бы у одного из игроков соберутся
все карты одной масти.
- 1.
- Из колоды в 36 карт (4 масти по 9 карт)
наудачу и без возвращения выбираются 7 карт. Найти вероятность того, что
попадется не менее двух тузов.
- 2.
- На отрезок [0,2] наудачу и независимо друг от друга
брошены две точки с координатами
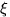 и
и 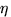 . Проверить, являются
ли события
. Проверить, являются
ли события 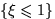 и
и 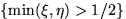 независимыми.
независимыми.
- 3.
- Пять раз подбрасываются три игральные кости.
Какова вероятность того, что сумма очков, равная 4, выпадет не более
трех раз?
- 4.
- В каждой урне по 5 шаров, при этом в первой 2 белых, во
второй — три, в третьей и четвертой — по 4 белых шара, остальные зеленые.
Из каждой урны наудачу выбирается шар. Известно, что три шара
оказались зелеными и один — белым.
Найти (условную) вероятность того, что из первой урны был выбран зеленый шар.
- 5.
- Из полной колоды карт (52 карты) вынимают одновременно четыре
карты. Рассматриваются события:
A={среди вынутых карт есть не менее двух пиковых};
B={среди вынутых карт есть хотя бы одна червонная}.
Найти вероятность объединения событий A и B .
- 6.
- Множество
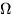 состоит из 15 элементов. Доказать,
что количество элементов в
состоит из 15 элементов. Доказать,
что количество элементов в 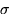 -алгебре всех подмножеств множества
-алгебре всех подмножеств множества 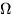 равно 215 .
равно 215 .
- 1.
- В новогоднем подарке по семь конфет пяти сортов, один из
которых — «Мишка косолапый».
Через дырочку мышке удалось достать десять конфет.
Найти вероятность того, что среди них не менее трех «Мишка косолапый».
- 2.
- На отрезок [0,3] наудачу и независимо друг от друга
брошены две точки с координатами
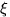 и
и 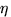 .Проверить, являются
ли события
.Проверить, являются
ли события 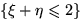 и
и 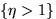 независимыми.
независимыми.
- 3.
- Двенадцать раз подбрасывается пара игральных костей.
Какова вероятность того, что сумма очков, равная 10, выпадет не более
трех раз?
- 4.
- Игральная кость A имеет две красных и четыре белых грани,
кость B — три красных и три белых, кость C — одну красную и пять
белых, и кость D — четыре красных и две белых. Кости брошены одновременно.
Известно, что ровно три из них выпали белыми гранями.
Найти (условную) вероятность того, что кость A выпала белой гранью.
- 5.
- Из ящика, в котором по семь белых, синих и красных
шаров, вынимают одновременно пять шаров. Рассматриваются события:
A={среди вынутых шаров есть белые};
B={среди вынутых карт есть не менее трех красных}.
Найти вероятность объединения событий A и B .
- 6.
- По 10 ящикам раскладывают 11 шариков. Предполагается, что
для каждого шарика равновозможно попасть в любой из ящиков. Найти вероятность
того, что ровно два ящика останутся пустыми.
- 1.
- Из колоды в 52 карты (4 масти по 13 карт) наудачу и
без возвращения выбираются 9 карт. Найти вероятность того, что
попадется не более семи карт бубновой масти.
- 2.
- На отрезок [0,2] наудачу и независимо друг от друга
брошены две точки с координатами
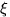 и
и 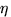 .Проверить, являются
ли события
.Проверить, являются
ли события 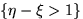 и
и 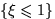 независимыми.
независимыми.
- 3.
- Восемь раз подбрасываются три игральные кости.
Какова вероятность того, что сумма очков, равная 17, выпадет не менее
семи раз?
- 4.
- Первый из четырех студентов правильно решает задачу
с вероятностью 0,8, второй — 0,5, третий — 0,6
и четвертый — с вероятностью 0,7. При проверке оказалось, что из
четырех решений ровно три правильных. Найти (условную)
вероятность того, что четвертый студент правильно решил задачу.
- 5.
- В урне 7 белых и 9 черных шаров. Из урны без возвращения
вынимают 6 шаров.
Найти вероятность того, что среди вынутых шаров будет больше черных,
чем белых.
- 6.
- Пусть
![$\Omega=[0,1]$](k1-271/img20.gif) ,
, 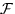 —
—
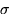 -алгебра борелевских множеств,
-алгебра борелевских множеств, 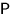 —
мера Лебега на отрезке [0,1] и
—
мера Лебега на отрезке [0,1] и ![$A=[1/2,\,1]$](k1-271/img23.gif) .Построить события B и C такие, что
.Построить события B и C такие, что 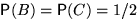 ,причем события A , B и C независимы в совокупности.
,причем события A , B и C независимы в совокупности.
- 1.
- На складе 15 мешков муки высшего сорта, 18 — первого
и 7 — второго сорта. Кладовщик наудачу выбирает и выдает восемь мешков.
Найти вероятность того, что
попадется не менее двух мешков муки высшего сорта.
- 2.
- На отрезок [0,3] наудачу и независимо друг от друга
брошены две точки с координатами
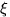 и
и 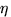 .Проверить, являются ли события
.Проверить, являются ли события 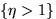 и
и 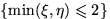 независимыми.
независимыми.
- 3.
- Одиннадцать раз подбрасывается пара игральных костей.
Какова вероятность того, что сумма очков, равная 10, выпадет не более
трех раз?
- 4.
- В каждой урне по 7 шаров, при этом в первой 4 белых, во
второй — два, в третьей и четвертой — по 5 белых шаров, остальные черные.
Из каждой урны наудачу выбирается шар. Известно, что три шара
оказались белыми и один — черным.
Найти (условную) вероятность того, что из третьей урны был выбран белый шар.
- 5.
- Два стрелка, независимо один от другого, делают по три выстрела
каждый по своей мишени. Вероятность попадания в мишень при одном выстреле
для первого стрелка 1/2, для второго — 1/3.
Найти вероятность того, что в мишени второго стрелка будет не меньше пробоин,
чем в мишени первого.
- 6.
- Какова минимальная
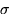 -алгебра подмножеств
-алгебра подмножеств 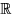 ,
содержащая все интервалы
,
содержащая все интервалы 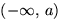 при любых вещественных a ?
Ответ обосновать.
при любых вещественных a ?
Ответ обосновать.
- 1.
- В коробке — 4 красных и по 8 белых и синих шаров.
Наудачу и без возвращения выбирают 6 шаров. Найти вероятность того, что
попадется не менее трех красных шаров.
- 2.
- На отрезок [0,2] наудачу и независимо друг от друга
брошены две точки с координатами
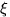 и
и 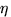 . Проверить, являются
ли события
. Проверить, являются
ли события 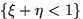 и
и 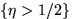 независимыми.
независимыми.
- 3.
- Семь раз подбрасывается пара игральных костей.
Какова вероятность того, что сумма очков, равная трем, выпадет не менее
трех, но не более шести раз?
- 4.
- Игральная кость A имеет одну красную грань,
кость B — три, кость C — две и кость D — четыре красных грани.
Остальные грани на всех костях белые.
Кости брошены один раз, при этом одна кость выпала белой гранью, а
остальные красными.
Найти (условную) вероятность того, что кость A выпала белой гранью.
- 5.
- Из полной колоды карт (52 карты) вынимают одновременно пять
карт. Рассматриваются события:
A={среди вынутых карт есть не менее двух бубей};
B={среди вынутых карт есть хотя бы одна пиковая}.
Найти вероятность объединения событий A и B .
- 6.
- Монета, которая может выпадать гербом, решкой или вставать
на ребро, подбрасывется дважды. Описать пространство элементарных исходов
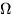 (перечислить его элементы) и построить минимальную
(перечислить его элементы) и построить минимальную 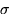 -алгебру,
содержащую события
A={при первом подбрасывании монета встала на ребро} и
B={ни разу монета не встала на ребро}.
-алгебру,
содержащую события
A={при первом подбрасывании монета встала на ребро} и
B={ни разу монета не встала на ребро}.
- 1.
- Из колоды в 36 карт (4 масти по 9 карт)
наудачу и без возвращения выбираются 9 карт. Найти вероятность того, что попадется не менее двух красных карт.
- 2.
- На отрезок [-1,2] наудачу и независимо друг от друга
брошены две точки с координатами
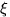 и
и 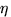 . Проверить, являются
ли события
. Проверить, являются
ли события 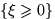 и
и 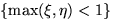 независимыми.
независимыми.
- 3.
- Десять раз подбрасываются три игральные кости.
Какова вероятность того, что сумма очков, равная 17, выпадет не более
двух раз?
- 4.
- Четыре стрелка A , B , C и D попадают по мишени
с вероятностями 0,4, 0,5, 0,2 и 0,8 соответственно, независимо друг
от друга. Известно, что после залпа в мишени оказалось три пробоины.
Найти (условную) вероятность того, что стрелок B попал.
- 5.
- В урне 8 белых и 5 черных шаров. Из урны без возвращения
вынимают 6 шаров.
Найти вероятность того, что среди вынутых шаров черных будет не больше,
чем белых.
- 6.
- Пусть
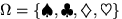 ,и
,и 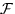 —
— 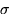 -алгебра всех подмножеств
-алгебра всех подмножеств 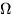 . Задать на
. Задать на
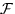 какую-нибудь вероятностную меру
какую-нибудь вероятностную меру 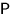 так, чтобы вероятность
события
так, чтобы вероятность
события 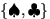 равнялась 1/8 .
равнялась 1/8 .
This document was generated using the
LaTeX2HTML translator Version 97.1 (release) (July 13th, 1997)