PREVIOUS SECTION: Properties of UI
In this section, we assume that random variables are not
necessary real-valued, but may take values in some measurable
space ![]() that is assumed to be complete separable metric space.
that is assumed to be complete separable metric space.
Coupling inequality
Let ![]() be two
be two ![]() -valued r.v.'s.
-valued r.v.'s.
Put ![]()
Then, for ![]() ,
,
|
|||
|
|||
Therefore, for any ![]() ,
, ![]() ,
that is
,
that is
Maximal coupling
Let's reformulate the statement. Note that l.h.s. of
inequality (*) depends on "marginal" distributions ![]() and
and ![]() only and does not
depend on the joint distribution of
only and does not
depend on the joint distribution of ![]() and
and ![]() . Therefore, we get the following:
. Therefore, we get the following:
for given ![]() and
and ![]() and for any their
coupling (*) takes place. Or, equivalently,
and for any their
coupling (*) takes place. Or, equivalently,
(?) May be, in ![]() is equality?
is equality?
(??) If "yes", then does there exists such a coupling that
![]()
Both answers are positive! And this is the statement of Dobrushin's theorem.
Proof. ![]() is a signed measure.
Therefore, Banach theorem states that
is a signed measure.
Therefore, Banach theorem states that
there exists a subset ![]() :
:
(a)
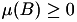
;
(b)
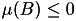
.
Note:
1) if ![]() , then
, then ![]() and the coupling is
obvious;
and the coupling is
obvious;
2) ![]() .
.
Assume ![]() . Introduce 4
distributions (probability measures):
. Introduce 4
distributions (probability measures):
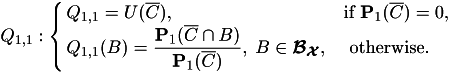
![]()
Similarly,
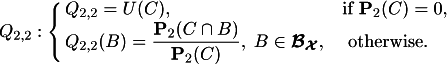
![]()
Then, define 5 independent r.v.'s: ![]() and
and
| |
1 | 2 | 0 |
| |
|
|
Now we can "construct" ![]() and
and ![]() :
:
![]()
![]()
Simple calculations show that ![]() ,
, ![]() .
.
| Problem No.3. "Indeed, . . ." |
Then,
![]()
So,
![]()
and the proof is completed.
QDE
NEXT SECTION: Probabilistic Metrics
File translated from TEX by TTH, version 1.58, Htex, and with Natalia Chernova as the TeX2gif-convertor.