Пусть
![]() — оценка параметра
— оценка параметра ![]() , полученная
по методу моментов, причем функция
, полученная
по методу моментов, причем функция
![]() непрерывна. Тогда
непрерывна. Тогда ![]() состоятельна.
состоятельна.
Пусть
![]() — оценка параметра
— оценка параметра ![]() , полученная
по методу моментов, причем функция
, полученная
по методу моментов, причем функция
![]() непрерывна. Тогда
непрерывна. Тогда ![]() состоятельна.
состоятельна.
Доказательство теоремы 3.
По ЗБЧ Хинчина имеем:
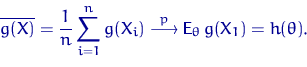
Поскольку функция ![]() непрерывна, то и
непрерывна, то и
![]()
Q.D.E.
Если полученные разумным путем оценки обязаны быть состоятельными, то свойство несмещенности — скорее исключение, нежели правило.
Действительно, несмещенность ОММ вида
![]() означала бы, что при всех
означала бы, что при всех
![]() выполнено равенство
выполнено равенство
| (5) |
Рассмотрим, к примеру, последовательность оценок для неизвестного параметра
![]() равномерного на отрезке
равномерного на отрезке ![]() распределения, полученную
в примере 4 и исследуем напрямую их свойства.
распределения, полученную
в примере 4 и исследуем напрямую их свойства.
Состоятельность:
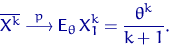
Поскольку функция ![]() непрерывна для всех
непрерывна для всех ![]() , то
при
, то
при ![]()
![\begin{displaymath}
\theta^*_k=\sqrt[k]{(k+1)\overline {X^k}} \buildrel {p} \over \longrightarrow \sqrt[k]{(k+1)
\dfrac{\theta^k}{k+1}}=\theta.\end{displaymath}](img276.gif)
Несмещенность:
т.е. оценка ![]() несмещенная.
несмещенная.
![]()
тогда как по свойству 2
![]()
Равенство ![]() означало бы, что для случайной величины
означало бы, что для случайной величины
![]() выполнено
выполнено ![]() , а для величины
, а для величины ![]() выполнено
выполнено
![]() или
или ![]() .
.
Но величина ![]() имеет невырожденное (более того, абсолютно
непрерывное) распределение. Поэтому оценка
имеет невырожденное (более того, абсолютно
непрерывное) распределение. Поэтому оценка ![]() — смещенная.
— смещенная.
Такими же смещенными
будут и оценки ![]() . Докажите это, воспользовавшись,
как в (5), неравенством Йенсена.
. Докажите это, воспользовавшись,
как в (5), неравенством Йенсена.
То есть вся последовательность
![]() состоит из состоятельных оценок, при этом только оценка
состоит из состоятельных оценок, при этом только оценка
![]() — несмещенная.
— несмещенная.
N.I.Chernova