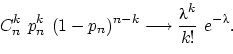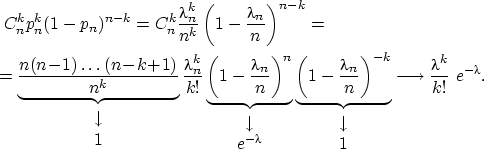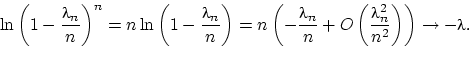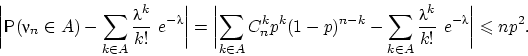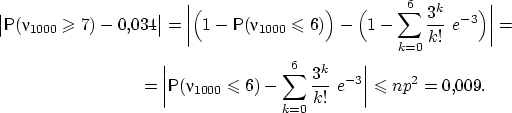Предположим, нам нужна вероятность получить не менее
семи успехов в тысяче испытаний
схемы Бернулли с вероятностью
успеха 0,003. Вероятность этого события равна любому
из следующих выражений, вычислить которые довольно сложно:

Сформулируем теорему о приближённом вычислении вероятности
какого-либо числа успехов в большом числе испытаний схемы Бернулли
с маленькой вероятностью успеха. Термин «большое число»
должен означать  . Если при этом
. Если при этом 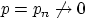 ,
то, очевидно, вероятность получить любое конечное число успехов
при растущем числе испытаний стремится к нулю. Необходимо чтобы
вероятность успеха
,
то, очевидно, вероятность получить любое конечное число успехов
при растущем числе испытаний стремится к нулю. Необходимо чтобы
вероятность успеха 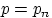 стремилась к нулю одновременно с ростом числа
испытаний. Но от испытания к испытанию вероятность успеха меняться
не может (см. определение схемы Бернулли). Поэтому нам придётся рассмотреть
так называемую «схему серий»: если испытание одно, то вероятность успеха в нём
равна
стремилась к нулю одновременно с ростом числа
испытаний. Но от испытания к испытанию вероятность успеха меняться
не может (см. определение схемы Бернулли). Поэтому нам придётся рассмотреть
так называемую «схему серий»: если испытание одно, то вероятность успеха в нём
равна 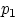 , если испытаний два, то вероятность успеха в каждом —
, если испытаний два, то вероятность успеха в каждом — 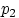 , и т.д.
Если испытаний
, и т.д.
Если испытаний  , то в каждом из них вероятность успеха равна
, то в каждом из них вероятность успеха равна 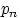 .
Вероятность успеха меняется не внутри одной серии испытаний,
а от серии к серии, когда меняется общее число испытаний.
.
Вероятность успеха меняется не внутри одной серии испытаний,
а от серии к серии, когда меняется общее число испытаний.
По
теореме 15 можно приближённо посчитать
вероятность получить не менее семи успехов в тысяче испытаний схемы Бернулли с вероятностью
успеха 0,003, с вычисления которой мы начали.
Поскольку

«велико», а

«мало»,
то, взяв

, можно записать приближённое равенство
 | (9) |
Осталось решить, а достаточно ли 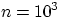 велико, а
велико, а  мало, чтобы заменить
точную вероятность
мало, чтобы заменить
точную вероятность  на приближённое значение
на приближённое значение
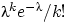 . Для этого нужно уметь оценивать
разницу между этими двумя вероятностями.
. Для этого нужно уметь оценивать
разницу между этими двумя вероятностями.
Следующую очень полезную теорему мы, исключительно из экономии времени, доказывать не станем.
Таким образом,
теорема 16 предоставляет нам возможность
самим решать, достаточно ли

велико, а

мало,
руководствуясь полученной величиной погрешности. Какова же погрешность
в формуле
(9)? Взяв

, имеем:
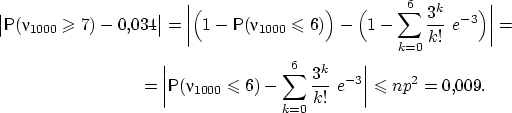
Можно утверждать, что искомая вероятность заключена в границах
(0,034 - 0,009, 0,034 + 0,009) = (0,025, 0,043).
На самом деле можно уточнить оценку в теореме 16. Например,
можно доказать, что погрешность даже меньше, чем 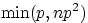 . В нашем примере это втрое
уменьшает оценку для погрешности —0,003 вместо 0,009,
уточняя границы для истинной вероятности: (0,031, 0,037).
. В нашем примере это втрое
уменьшает оценку для погрешности —0,003 вместо 0,009,
уточняя границы для истинной вероятности: (0,031, 0,037).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

![]() . Если при этом
. Если при этом ![]() ,
то, очевидно, вероятность получить любое конечное число успехов
при растущем числе испытаний стремится к нулю. Необходимо чтобы
вероятность успеха
,
то, очевидно, вероятность получить любое конечное число успехов
при растущем числе испытаний стремится к нулю. Необходимо чтобы
вероятность успеха ![]() стремилась к нулю одновременно с ростом числа
испытаний. Но от испытания к испытанию вероятность успеха меняться
не может (см. определение схемы Бернулли). Поэтому нам придётся рассмотреть
так называемую «схему серий»: если испытание одно, то вероятность успеха в нём
равна
стремилась к нулю одновременно с ростом числа
испытаний. Но от испытания к испытанию вероятность успеха меняться
не может (см. определение схемы Бернулли). Поэтому нам придётся рассмотреть
так называемую «схему серий»: если испытание одно, то вероятность успеха в нём
равна ![]() , если испытаний два, то вероятность успеха в каждом —
, если испытаний два, то вероятность успеха в каждом — ![]() , и т.д.
Если испытаний
, и т.д.
Если испытаний ![]() , то в каждом из них вероятность успеха равна
, то в каждом из них вероятность успеха равна ![]() .
Вероятность успеха меняется не внутри одной серии испытаний,
а от серии к серии, когда меняется общее число испытаний.
.
Вероятность успеха меняется не внутри одной серии испытаний,
а от серии к серии, когда меняется общее число испытаний.