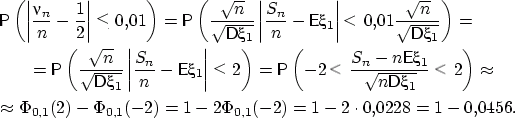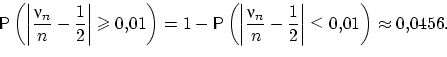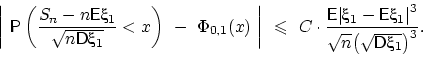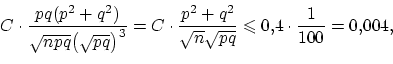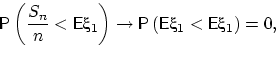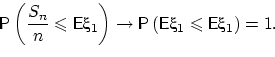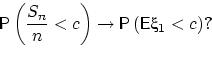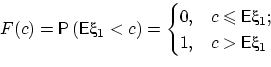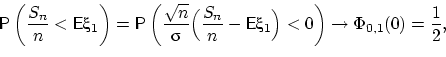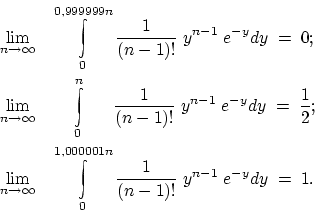



Next: Характеристические функции
Up: Центральная предельная теорема
Previous: Предельная теорема Муавра
Пример 57.
Задача из
примера 55.
Монета подбрасывается 10000 раз. Оценим вероятность того, что
частота выпадения герба отличается от половины на одну сотую или более.
Решение. Требуется найти
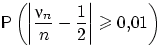 ,
где
,
где 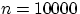 ,
, 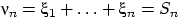 — число выпадений герба, а
— число выпадений герба, а
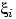 — независимые случайные величины, имеющие одно и то же распределение Бернулли
с параметром 1/2. Вычислим вероятность дополнительного события. Домножим обе части
неравенства под знаком вероятности на
— независимые случайные величины, имеющие одно и то же распределение Бернулли
с параметром 1/2. Вычислим вероятность дополнительного события. Домножим обе части
неравенства под знаком вероятности на 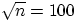 и поделим на корень из
дисперсии
и поделим на корень из
дисперсии 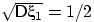 .
.
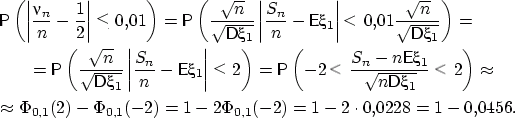
Искомая вероятность примерно равна 0,0456:
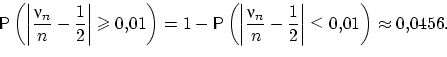
Центральной предельной теоремой пользуются для приближённого вычисления
вероятностей, связанных с суммами большого числа
независимых и
одинаково распределённых
величин. При этом распределение центрированной и нормированной суммы
заменяют на
стандартное нормальное распределение.
Насколько велика ошибка при такой замене (погрешность приближения)?
Упражнение 54.
Какие ещё предельные теоремы для
схемы Бернулли вы знаете? Что такое теорема
Пуассона? Найти её. Какова погрешность пуассоновского приближения? Вычислить
её. Объяснить, исходя из полученной величины, почему
теорема Пуассона
не применима в задаче из
примера 57.
В
примере 57 мы вычислили искомую вероятность тоже не точно, а
приближённо — взгляните на равенство «
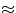
»
и спросите себя: насколько мы ошиблись? Стоит ли доверять ответу
«0,0456»?
Следующий результат позволяет оценить погрешность приближения в ЦПТ.
Теорема 39 (неравенство Берри — Эссеена).
В условиях
ЦПТ для любого

и для любого распределения

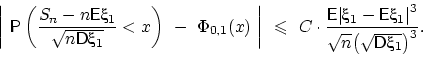
Продолжение
примера 57. Проверьте, что для случайной величины

с
распределением Бернулли

Поэтому разница между левой и правой частями приближённого
равенства «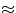 » в примере 57
при
» в примере 57
при 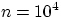 и
и 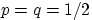 не превышает величины
не превышает величины
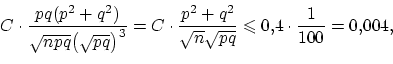
так что искомая вероятность
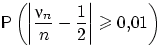 не больше, чем 0,0456 + 0,004.
Уместно сравнить этот ответ с оценкой, полученной с помощью ЗБЧ
в примере 55.
не больше, чем 0,0456 + 0,004.
Уместно сравнить этот ответ с оценкой, полученной с помощью ЗБЧ
в примере 55.
Следующая проблема связана с распространённейшим среди
студентов
заблуждением, которое выглядит так: при

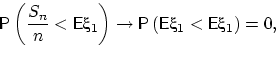
но уже
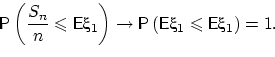
Пример 58.
Пусть

—
независимые и
одинаково распределённые случайные величины
с конечной и
ненулевой дисперсией 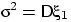
,
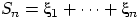
— сумма первых

случайных величин. При каких

имеет или не имеет место
сходимость
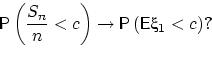
Решение.
Согласно ЗБЧ, последовательность 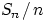 сходится по вероятности,
а, следовательно, и слабо, к
сходится по вероятности,
а, следовательно, и слабо, к  .
.
Слабая сходимость означает, что последовательность функций распределения
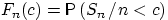 сходится к функции распределения
сходится к функции распределения
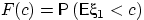 , если
, если 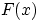 непрерывна
в точке
непрерывна
в точке  (и ничего не означает, если
(и ничего не означает, если 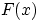 разрывна в точке
разрывна в точке  ). Но
). Но
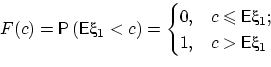
есть функция распределения вырожденного закона и непрерывна
в любой точке  , кроме
, кроме 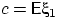 .
.
Итак, первый вывод: сходимость
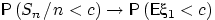 имеет место для любого
имеет место для любого  , кроме, возможно,
, кроме, возможно, 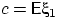 .
.
Убедимся, что для 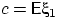 такой сходимости быть не может.
Согласно ЦПТ,
такой сходимости быть не может.
Согласно ЦПТ,
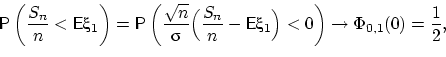
тогда как 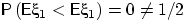 .
Аналогично, кстати, ведёт себя и вероятность
.
Аналогично, кстати, ведёт себя и вероятность
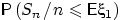 . Она тоже стремится к 1/2,
а не к
. Она тоже стремится к 1/2,
а не к 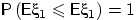 .
.
И изящное упражнение на ту же тему:
N.Ch.
![]() ,
где
,
где ![]() ,
, ![]() — число выпадений герба, а
— число выпадений герба, а
![]() — независимые случайные величины, имеющие одно и то же распределение Бернулли
с параметром 1/2. Вычислим вероятность дополнительного события. Домножим обе части
неравенства под знаком вероятности на
— независимые случайные величины, имеющие одно и то же распределение Бернулли
с параметром 1/2. Вычислим вероятность дополнительного события. Домножим обе части
неравенства под знаком вероятности на ![]() и поделим на корень из
дисперсии
и поделим на корень из
дисперсии ![]() .
.